図形の面積の問題でいつも不思議に思っていることがあります。

それは「正三角形の面積」を求める問題が、中学３年生の「三平方の定理」を学習してから勉強することです。

理由は簡単で、底辺から高さを求めることが「三平方の定理」を使わないとできないからです。

でも、小学生でも解く方法があります。それが今回紹介する「直角三角形の３辺の比」になります。

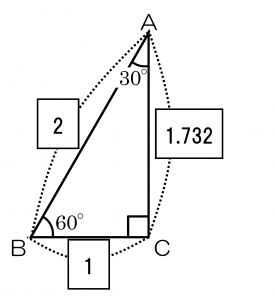
90°、60°、30°の直角定規の辺の比は「2：1：1.732」と決まっています。この中で、1：1.732という比は「白金比」として良く知られています。

円周率3.14は小学校で学習するのに、白金比1.732を小学校で学習しないのは、もったいないと思うのは私だけでしょうか。

この1.732を知っていると、次のような正三角形の面積が小学生でも解けてしまうのです。

底辺は4cm、高さは底辺の半分2cmの1.732倍で3.464cm、面積は4×3.464÷2=6.928㎠となります。

小数の計算が苦手だとちょっと大変ですが、円周や円の面積と同じように「正三角形の高さ＝底辺÷２×1.732」で求めることが可能です。

中学３年生になると、1.732→√3という根号で表すことになり、計算が少し楽になります。

このように、円周率3.14だけでなく白金比1.732を知っておくと、面積の世界がぐっと広がっていきます。