先日の模擬テストの問題がおもしろいと思ったので、ご紹介。(特殊文字使用。Windowsならちゃんと見られると思う。)
==============================================================================
【問題】
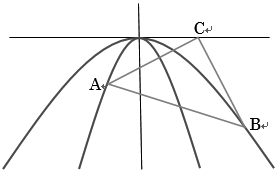
y=2ax² (a<0)のグラフ上にx=-2となる点Aがあり、y=ax² のグラフ上にx=4となる点Bがある。
また、x軸上に点Cがあり、△ABCが∠C=90°の直角二等辺三角形であるとき、点Cのx座標を求めなさい。
==============================================================================
ちなみに私は、この問題の「直角二等辺三角形」というところの「二等辺」のところを読み落としてしまった・・・というよりも見過ごしてしまったため、はじめ、あらぬ方向へ解法を進めてしまった。集中してじっくりちゃんと読むことが何よりも重要だ。
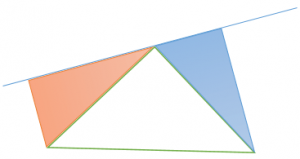この問題を解決するポイントは、左の図。たいていの参考書の合同の応用の項目には例題などにこのような図形が紹介されており、オレンジ色の三角形と水色の三角形が合同であることを証明する問題を題材としている。
実はこの問題にこの形が隠れていることにどれだけの子供が気づくのだろうか。勉強をするときに、解き方と答えだけを追いかけルような勉強の仕方では太刀打ちできない。「直角の頂点を直線が貫くときにこのようなことが起こる」ということを考え、そこに感銘しなければ心にとどまらない。そう、数学の中に見え隠れする「意味」や「美」に気づいたり感動したりする、心の力、「心力」が必要なのだ。
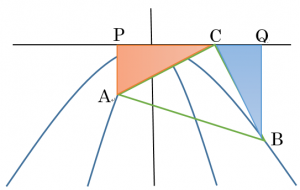
ちなみに、解法のポイントは以下の通り。
A(-2,8a) B(4,16a) P(-2.0) Q(4,0) となる。
CをC(x,0)とすれば、
PA = CQ なので、0-8a = 4-x ・・・①
PC = QB なので、x-(-2) = 0-16a ・・・②
このaとxの連立方程式を解けばよい。
